Hello everyone,
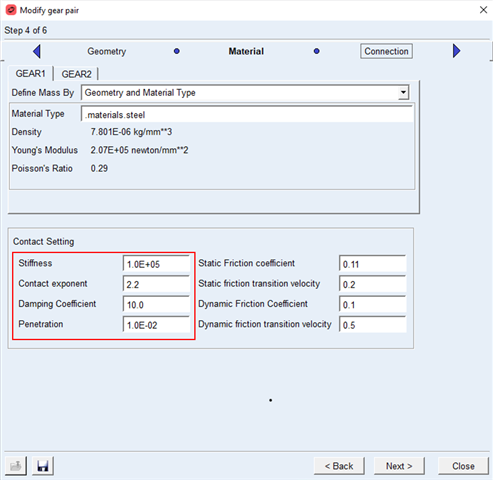
I am working on modeling a differential with a bevel gear pair using a 3D contact method, and I need guidance on setting up the contact parameters, particularly the damping coefficient, when the gear pair is operating in oil.
Thank you in advance for your help!