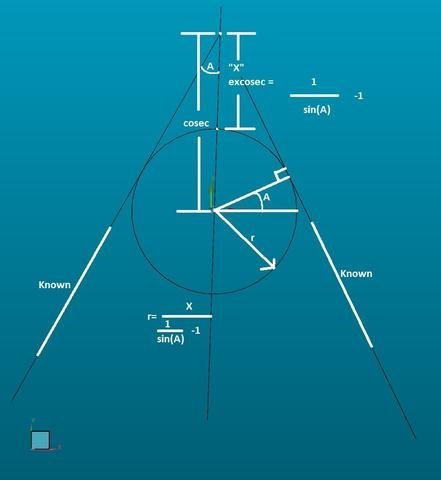
As long as two tangent faces can be measured/determined, all that is required to infer a radius is 1 point. 1 point is taken on the mid line of the two faces to determine the excosec and a little bit of algebra later you have a radius.
$$ NO,
[B] ASSUMPTION: BOTH FACES ARE CO-TANGENT TO RADIUS[/B]
[B] edit: i suppose the second assumption would be "the radius has perfect form"[/B]
$$ NO,
[B] Two line measurements are taken.
One on either tangent of the corner radius with
vectors pointing towards the radius being measured.
The vector nominals in the command block screw with
the construction of LIN3, otherwise the code as is would not
matter what orientation it is in.
(wont be a problem in real program)
Could probably fix with expressions in vectors
Manual mode for demonstration purposes only.[/B]
LIN1 =FEAT/LINE,CARTESIAN,UNBOUNDED
THEO/<18.839,0,10>,<1,0,0>
ACTL/<-119.063,-114.215,11.302>,<0.4934556,0.869771,0>
MEAS/LINE,2,ZPLUS
HIT/BASIC,NORMAL,<18.839,0,10>,<0,1,0>,<-119.063,-114.215,11.337>,USE THEO=YES
HIT/BASIC,NORMAL,<108.2,0,10>,<0,1,0>,<5.926,106.092,11.266>,USE THEO=YES
ENDMEAS/
LIN2 =FEAT/LINE,CARTESIAN,UNBOUNDED
THEO/<100,-103.413,10>,<0,1,0>
ACTL/<121.972,-136.12,11.265>,<-0.4351452,0.9003603,0>
MEAS/LINE,2,ZPLUS
HIT/BASIC,NORMAL,<100,-103.413,10>,<1,0,0>,<121.972,-136.12,11.265>,USE THEO=YES
HIT/BASIC,NORMAL,<100,-23.975,10>,<1,0,0>,<17.756,79.513,11.265>,USE THEO=YES
ENDMEAS/
MODE/DCC
$$ NO,
[B] Construct the point of intersection[/B]
PNT1 =FEAT/POINT,CARTESIAN,NO
THEO/<100,0,10>,<1,0,0>
ACTL/<5.377,105.125,11.284>,<0.4934556,0.869771,0>
[B] CONSTR/POINT,INT,LIN1,LIN2[/B]
$$ NO,
[B] Construct a mid line to use for vectors on pnt2.[/B]
LIN3 =FEAT/LINE,CARTESIAN,UNBOUNDED,NO
THEO/<54.527,-45.473,10>,<0.7071068,0.7071068,0>
ACTL/<-2.198,-124.836,11.284>,<0.0329234,0.9994579,0>
[B] CONSTR/LINE,MID,LIN1,LIN2[/B]
$$ NO,
[B] This constructed line isnt necessary and could be removed.
A replacement could be the use of ANGLEBETWEEN()
but the result would need converted back into vectors.
Dont care enough to do that atm.
Something with UNIT() maybe. note to self, wtf is CROSS(,)[/B]
CHECK/100,1
TOUCHSPEED/ 20
PREHIT/2
$$ NO,
[B] Flip pnt2 vector expresions to negative and add a large
complimentary PREHIT distance if you would like this
to measure inside rads
... pretty sure that should do it.[/B]
PNT2 =FEAT/POINT,CARTESIAN
THEO/<120,0,10>,<[B]LIN3.I,LIN3.J,LIN3.K[/B]>
ACTL/<3.513,48.49,11.281>,<0.0329234,0.9994579,0>
MEAS/POINT,1,WORKPLANE
HIT/BASIC,NORMAL,<[B]PNT1.X,PNT1.Y,PNT1.Z[/B]>,<[B]LIN3.I,LIN3.J,LIN3.K[/B]>,<3.513,48.49,11.281>,USE THEO=YES
ENDMEAS/
CHECK/0,1
DIM LOC1= POSITION OF POINT PNT2 UNITS=MM ,$
GRAPH=OFF TEXT=OFF MULT=10.00 OUTPUT=[B]NONE[/B] FIT TO DATUMS=OFF DEV PERPEN CENTERLINE=OFF DISPLAY=DIAMETER
AX MEAS NOMINAL +TOL -TOL BONUS DEV OUTTOL
X 3.513 [B]PNT1.X[/B] -1.864
Y 48.490 [B]PNT1.Y[/B] -56.635
TP 113.331 RFS [B]80085[/B].000 0.000 113.331 0.000 -------->
END OF DIMENSION LOC1
$$ NO,
[B] LOC1 is only used to get the distance from the intersecting point
to the measured point. However, loc1.tp.meas will always return
the diametric true position even if you change the display to radius.
Divide by 2[/B]
RAD1 =GENERIC/CIRCLE,DEPENDENT,CARTESIAN,OUT,$
NOM/XYZ,<0+0,0+0,0+0>,$
MEAS/XYZ,<[SIZE=16px][COLOR=#0000FF][B]PNT2.X+(-LIN3.I*RAD1.RADIUS)[/B][/COLOR][/SIZE],[SIZE=16px][COLOR=#0000FF][B]PNT2.Y+(-LIN3.J*RAD1.RADIUS)[/B][/COLOR][/SIZE],PNT2.Z>,$
NOM/IJK,<0,0,1>,$
MEAS/IJK,<0,0,1>,$
RADIUS/0,[SIZE=16px][COLOR=#0000FF][B](LOC1.TP.MEAS/2)/((1/SIN(DEG2RAD(ANGLEBETWEEN(LIN1.IJK,LIN2.IJK))/2))-1)[/B][/COLOR][/SIZE]
$$ NO,
[B] ^^The Bees Knees^^
That Parenthesis Pasta is ugly but it still works.
In the pursuit of visually displaying the radius in the correct position,
I have accidently measured the center of the radius as well. No, I dont know
why a feature referencing itself works.[/B]
DIM LOC2= LOCATION OF CIRCLE RAD1 UNITS=MM ,$
GRAPH=OFF TEXT=OFF MULT=10.00 OUTPUT=BOTH HALF ANGLE=NO
AX MEAS NOMINAL +TOL -TOL DEV OUTTOL
R 49.163 RAD1.RADIUS **** **** 0.000 0.000 #--------
END OF DIMENSION LOC2
$$ NO,
[B] was getting measurements under .001" deviation
Id give her a +/- .002" accuracy.
(as a complete guess, haven't done study yet)
Should be most accurate at 90 degrees total angle
with exponential increase in error at both limits.
Smaller internal angle will be affected by line measurement acc.
Larger internal angle will be affected by rad point measurement acc.
Outside radius should be slightly more accurate for smaller -wait... no one cares[/B]
