But what can you do if 100% of the components are measured anyway, and if necessary even bad components are sorted out?
A first inadequate statement would then be: "You don't need capability values". This is because a capability indicates how good or bad the components, that were not measured, are. (which is why poor measured values must also remain in the calculation in the case of random sampling, as these reflect a part of the population).
But let's start slowly. On the characteristic mask, a characteristic can be given the information that this is a 100% measurement technique:

Without an evaluation strategy behind it, however, this is nothing more than a nice piece of information on the characteristic mask.
In the requirements of the strategy, a sub-strategy can be defined which reacts to this setting of the characteristic mask:
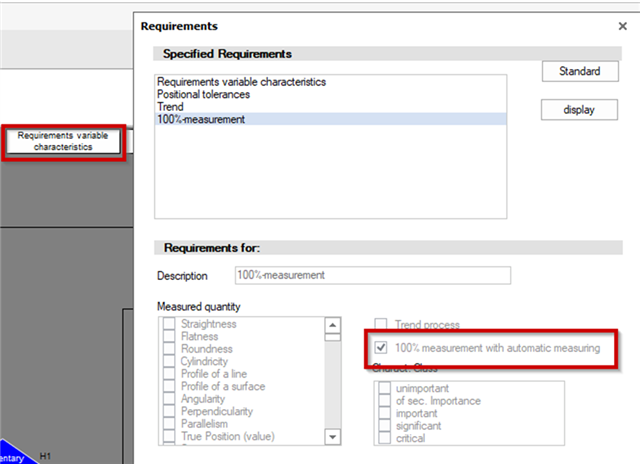
Possible requirements would be those:
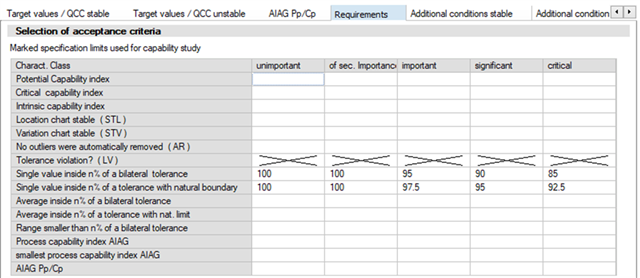
Basically, the activation of tolerance violations (as characteristics with only one specification limit do not have a % tolerance range) and, if necessary, restrict the % range for higher characteristics classes. With 2 specification limits, the higher the characteristic class, the smaller % range within the tolerance is taken into account (suggestion: consider measurement uncertainty...).
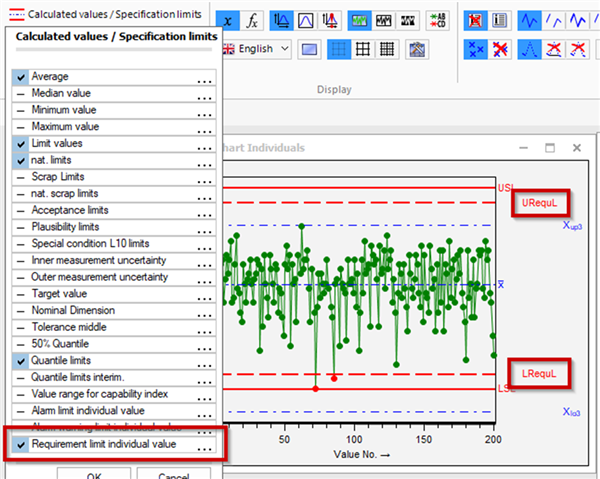
These limits could also be displayed in a value chart:
But do you need capabilities? The very clear answer to this is YO! (YO is a combination of Yes and nO)
The calculation of capabilities could be cancelled for such characteristics. However, the author has decided to leave this information as it is. Let's look at 2 characteristics. Both are "capable" as only the X% tolerance range is checked.
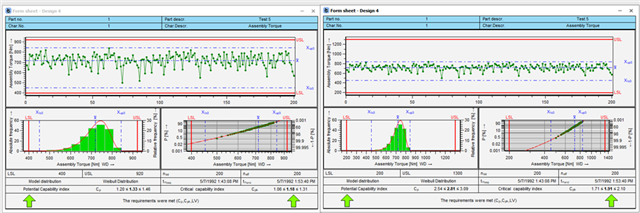
Both are "capable" because all measured values are within the % tolerance range. However, the capabilities can still provide information about how much space you still have.
It therefore remains to be considered:
Does the calculation of the capability index remain available as further information (without it being a requirement), and what % range does one monitor depending on characteristic class, possibly also taking into account the average measurement uncertainty.
