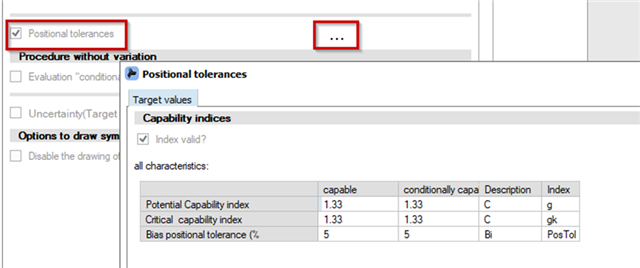
The question of an MSA for positional tolerances comes up very often. (and also as a question for the VDA5). For this reason, this should be listed here, but less as a "how to" and more as a "why to".
Firstly, the technical part: The evaluation of "multivariate characteristics" (and this includes positional tolerances) is only possible with type 1. Here, the mathematics for the multivariate evaluation was adapted to the MSA (comparison of tolerance ellipse to probability ellipse). In a strategy, however, this must still be permitted separately in type 1:
This is used in a technically sensible application for unbalances (unbalances are also multivariate evaluations).
However, the question of the "MSA" of items only arises because they simply exist in the test plan.
Let's move from the "how to" to the "why to" and ask consistent counter-questions:
When an MSA is performed, it is to determine whether the one measured value can be repeated accurately enough. As a repeat measurement, as a comparative measurement. So far so good. Familiar knowledge.
Now let's look at a positional tolerances.
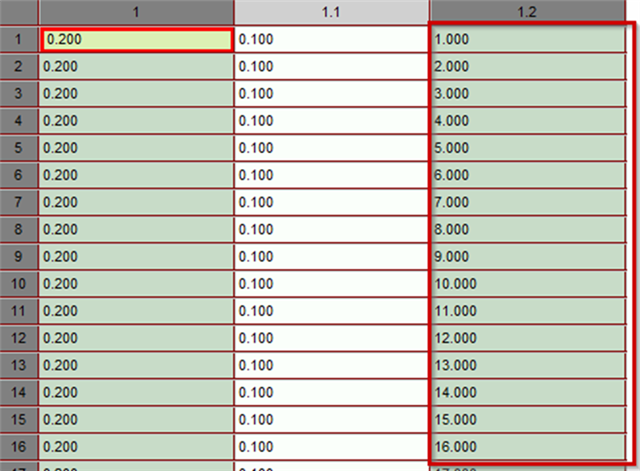
The first measured value was 0.2 (the deviation from target value centre of the position to the real measurement, in the diameter view. The deviations itself as a radius is 0.1)
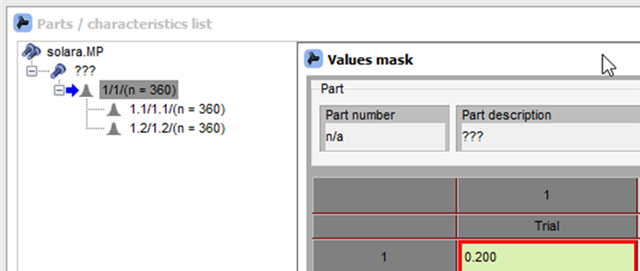
Interestingly, we now measure this 0.2 repeatedly and precisely:
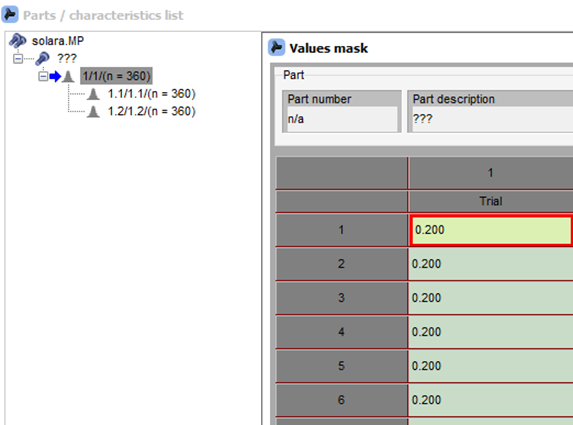
But what did we measure with the "0.2"? The "true position" (as a radius of 0.1)!
If you now look at the XY plot of the positional tolerances, you can see that in this fictitious example a circle was drawn with 360 measured values:
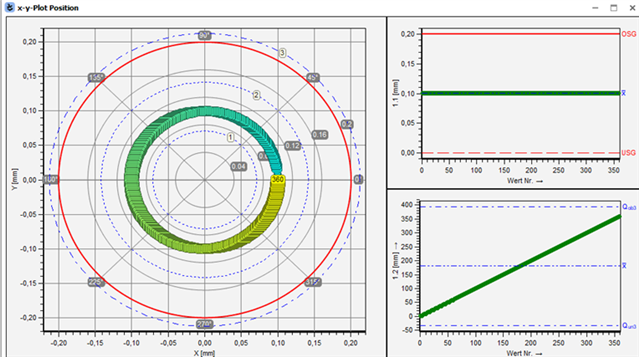
Each value deviates exactly 0.1 from the centre. But at different angles! The value at 90° and the value at 270° degrees (both 0.2 in the "true position", as positions are output as diameters and not as radii) therefore have a difference of 0.2, a fact that is ignored by the pure consideration of the "true position".
The values mask of the fictitious example, written in polar notation, always shows the amount of deviation and the angle to the angle, which is ignored in the evaluation of only the "true position".
Even in the machine capability and process analysis, no attention is paid to the "evaluation of the amount". So why should an MSA be carried out for the "true position"? Only the MSA (or the measurement uncertainty according to VDA5) of the axes makes sense.
It should be pointed out again at this point that this explanation does NOT refer to type 1 analysis for unbalance. Due to the completely different measuring technique, this is a valid analysis of the repeatability of a defined weighting at a defined angle. The "Type 1" is definitely applicable for unbalances, precisely because the analysis then also ignores the amount and calculates the distribution ellipse.
